Traffic Model

Have you ever been trapped in a traffic jam? Have you ever passed a traffic jam and found that there is no traffic accident or other obvious reason that might induce traffic jams? Congratulation! You are trapped in one of the most interesting physical phenomena called phantom traffic jamThis kind of jamming transition is fascinating since you can just ask some driver to drive on a circular track, and surprisingly, a jam is formed in this system. See the video below.

In order to understand this phantom traffic jam, various models have been proposed. Some describe a traffic system as a fluid, while some apply a particle-based model to illustrate. One classical model describes drivers as interacting particles. Each driver tries to drive with an optimal velocity $v_{\text{opt}}$. Such velocity might depend on the velocity of drivers, the relative velocity between drivers and the vehicle in front, or the inter-vehicle distance. The simplest one is assuming that drivers decide their velocity only by the inter-vehicle distance. That is, for $i-$th driver, the velocity $v_i(t)$ at time $t$ is $$v_i(t) = v_{\text{opt}}(\Delta x_i),$$ where $\Delta x_i = x_{i+1}-x_{i}$. However, since we are human, it is impractical to change the velocity of a vehicle without any reaction time. Therefore, by considering this reaction time $\tau$, the velocity of a driver should be $$v_i(t+\tau) = v_{\text{opt}}(\Delta x_i).$$ By applying Taylor expansion, the dynamical equation of each driver can be determined as $$ \frac{d v_i}{dt} = \frac{v-v_{\text{opt}}(\Delta x_i)}{\tau}. $$.

So far, we have yet to specify the optimal velocity of any function. However, there are some criteria that an optima velocity should satisfy:

1. Since it is impossible to drive at an infinite speed even when no vehicles are in front, thus, optimal velocity must be saturated as the inter-vehicle distance approaches infinity.
2. Since a driver must stop when the inter-vehicle distance is zero, thus, optimal velocity must be zero as the inter-vehicle is zero.

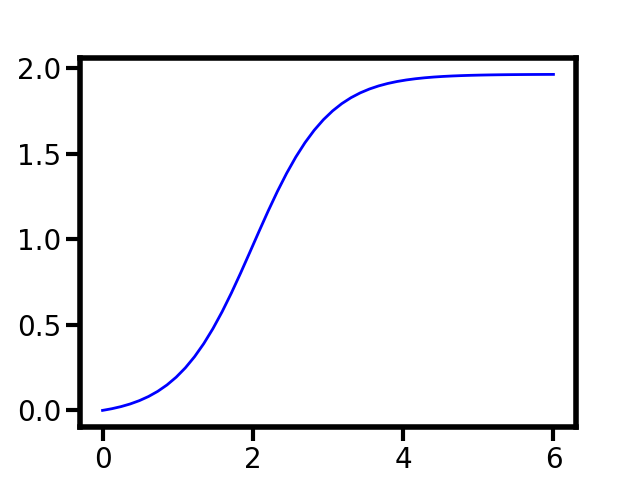
In 1995, Prof. Bando employed a shifted hyperbolic tangent to describe optimal velocity. See Fig. 1 below. The hyperbolic tangent is shifting because we expect that the acceleration rate should be smooth when the inter-vehicle distance remains small.

To show that such simple model can spontaneously generate traffic jam under a correct circumstances, I use python to simulate the system. The jupyter-notebook code is here (download link), and the complete code for finding various phenomenon, such as phase transition point, is place in my github. The simulation result is shown in the following video.

To understand the jamming transition analytically, we can employ linear analysis in this system. An apparent steady state of the system is that all drivers drive with their optimal velocities and are evenly distributed on the circular track.. By applying a small perturbation on the steady state and approaching the total number of vehicles to infinity while remaining at fixed density, we can find that the system will be unstable when $$ \tau > \frac{1}{2}\left(\frac{dv_{\text{opt}}(\Delta x)}{d\Delta x}\right)\Bigg|_{\Delta x = L/N}. $$ The physical interpretation of this stability condition is: The left-hand side is the reaction time of drivers. The right-hand side is the change rate of optimal velocity when the inter-distance of vehicles changes. This rate means the desired changing rate of drivers. However, in reality, their changing rate is their reaction time. When the reaction time is larger than the changing rate, drivers need more time to react to the change, and a slight perturbation will be amplified and become a jam.

Therefore, we can conclude that traffic jams are induced by the reaction time of drivers. A straightforward solution is developing identical self-driving cars to reduce the reaction time significantly. However, my research will show you that self-driving is great solution, but identical might not be a perfect solution.